Determinación de variación en línea. Varianza de una variable aleatoria discreta

Además de estudiar la variación de una característica en toda la población, a menudo es necesario rastrear cambios cuantitativos en la característica entre los grupos en los que se divide la población, así como entre grupos. Este estudio de variación se logra mediante el cálculo y análisis. varios tipos variaciones.
Hay variaciones totales, intergrupales e intragrupales..
Varianza total σ 2 Mide la variación de un rasgo en toda la población bajo la influencia de todos los factores que causaron esta variación.

La varianza intergrupal (δ) caracteriza la variación sistemática, es decir diferencias en el valor del rasgo estudiado que surgen bajo la influencia del factor rasgo que forma la base del grupo. Se calcula mediante la fórmula:
.

Varianza dentro del grupo (σ) refleja variación aleatoria, es decir parte de la variación que se produce bajo la influencia de factores no contabilizados y no depende del factor-atributo que forma la base del grupo. Se calcula mediante la fórmula:
.

Promedio de variaciones dentro del grupo: .

Existe una ley que conecta 3 tipos de dispersión. La varianza total es igual a la suma del promedio de la varianza dentro del grupo y entre grupos: .
Esta relación se llama regla para sumar variaciones.

Un indicador ampliamente utilizado en el análisis es la proporción de la varianza entre grupos en la varianza total. Se llama coeficiente empírico de determinación (η 2): .
La raíz cuadrada del coeficiente empírico de determinación se llama relación de correlación empírica (η):
.
Caracteriza la influencia de la característica que forma la base del grupo sobre la variación de la característica resultante. La relación de correlación empírica oscila entre 0 y 1.
vamos a mostrarlo uso práctico en siguiente ejemplo(Tabla 1).

Ejemplo No. 1. Tabla 1 - Productividad laboral de dos grupos de trabajadores en uno de los talleres de NPO Cyclone

Calculemos las medias y varianzas generales y grupales:

Los datos iniciales para calcular el promedio de la varianza intragrupo e intergrupo se presentan en la tabla. 2.
Tabla 2
Cálculo y δ 2 para dos grupos de trabajadores.

Grupos de trabajadores	Número de trabajadores, personas.	Promedio niños/turno	Dispersión
Formación técnica completa.	5	95	42,0
Quienes no hayan completado la formación técnica	5	81	231,2
todos los trabajadores	10	88	185,6

Calculemos los indicadores. Promedio de variaciones dentro del grupo:

.
Varianza intergrupal

Varianza total:
Así, la relación de correlación empírica: .

Junto con la variación en las características cuantitativas, también se puede observar variación en las características cualitativas. Este estudio de variación se logra calculando los siguientes tipos de varianzas:

La dispersión de la participación dentro del grupo está determinada por la fórmula

Dónde n yo– número de unidades en grupos separados.
La proporción de la característica estudiada en toda la población, que está determinada por la fórmula:
Los tres tipos de variación están relacionados entre sí de la siguiente manera:

Esta relación de varianzas se denomina teorema de la suma de varianzas del rasgo compartido.

Dispersión variable aleatoria es una medida de la dispersión de valores de esta cantidad. Una varianza baja significa que los valores están agrupados muy juntos. Una gran dispersión indica una fuerte dispersión de valores. El concepto de varianza de una variable aleatoria se utiliza en estadística. Por ejemplo, si compara la varianza de dos valores (como entre pacientes masculinos y femeninos), puede probar la importancia de una variable. La varianza también se utiliza al crear modelos estadísticos, ya que una varianza baja puede ser una señal de que se están sobreajustando los valores.

Pasos

Calcular la varianza de la muestra

Registre los valores de la muestra. En la mayoría de los casos, los estadísticos sólo tienen acceso a muestras de poblaciones específicas. Por ejemplo, como regla general, los estadísticos no analizan el costo de mantener la totalidad de todos los automóviles en Rusia, sino que analizan una muestra aleatoria de varios miles de automóviles. Esta muestra ayudará a determinar el costo promedio de un automóvil, pero lo más probable es que el valor resultante esté lejos del real.
- Por ejemplo, analicemos la cantidad de bollos vendidos en una cafetería durante 6 días, tomados en orden aleatorio. La muestra tiene siguiente vista: 17, 15, 23, 7, 9, 13. Esta es una muestra, no una población, porque no tenemos datos sobre los bollos vendidos cada día que la cafetería está abierta.
- Si le dan una población en lugar de una muestra de valores, continúe con la siguiente sección.
Escriba una fórmula para calcular la varianza muestral. La dispersión es una medida de la dispersión de valores de una determinada cantidad. Cómo valor más cercano dispersión es cero, más cerca se agrupan los valores entre sí. Cuando trabaje con la selección de valores, utilice la siguiente fórmula para calcular la varianza:
- s 2 (\displaystyle s^(2)) = ∑[(x yo (\displaystyle x_(i))- X) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))– esto es dispersión. La dispersión se mide en unidades cuadradas.
- x yo (\displaystyle x_(i))– cada valor de la muestra.
- x yo (\displaystyle x_(i)) necesitas restar x̅, elevarlo al cuadrado y luego sumar los resultados.
- x̅ – media muestral (media muestral).
- n – número de valores en la muestra.
Calcule la media muestral. Se denota como x̅. La media muestral se calcula como una media aritmética simple: sume todos los valores de la muestra y luego divida el resultado por el número de valores de la muestra.
- En nuestro ejemplo, suma los valores de la muestra: 15 + 17 + 23 + 7 + 9 + 13 = 84
  Ahora divide el resultado por el número de valores de la muestra (en nuestro ejemplo son 6): 84 ÷ 6 = 14.
  Media muestral x̅ = 14.
- La media muestral es el valor central alrededor del cual se distribuyen los valores de la muestra. Si los valores de la muestra se agrupan alrededor de la media muestral, entonces la varianza es pequeña; de lo contrario, la variación es grande.
Reste la media muestral de cada valor de la muestra. Ahora calcula la diferencia x yo (\displaystyle x_(i))- x̅, donde x yo (\displaystyle x_(i))– cada valor de la muestra. Cada resultado obtenido indica el grado de desviación de un valor particular de la media muestral, es decir, qué tan lejos está este valor de la media muestral.
- En nuestro ejemplo:
  x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
  x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
  x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
  x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
  x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
  x6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
- La exactitud de los resultados obtenidos es fácil de comprobar, ya que su suma debe ser igual a cero. Esto está relacionado con la definición de promedio, ya que los valores negativos (distancias del promedio a valores más pequeños) se compensan completamente con valores positivos (distancias del promedio a valores más grandes).
Como se señaló anteriormente, la suma de las diferencias x yo (\displaystyle x_(i))- x̅ debe ser igual a cero. Esto significa que la varianza media es siempre cero, lo que no da ninguna idea sobre la dispersión de los valores de una determinada cantidad. Para resolver este problema, eleva al cuadrado cada diferencia x yo (\displaystyle x_(i))- X. Esto dará como resultado que solo obtenga números positivos, que nunca sumarán 0.
- En nuestro ejemplo:
  (x 1 (\displaystyle x_(1))- X) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
  (x 2 (\displaystyle (x_(2))- X) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
  9 2 = 81
  (-7) 2 = 49
  (-5) 2 = 25
  (-1) 2 = 1
- Encontraste el cuadrado de la diferencia - x̅) 2 (\displaystyle ^(2)) para cada valor de la muestra.
Calcula la suma de los cuadrados de las diferencias. Es decir, encuentra esa parte de la fórmula que se escribe así: ∑[( x yo (\displaystyle x_(i))- X) 2 (\displaystyle ^(2))]. Aquí el signo Σ significa la suma de diferencias al cuadrado para cada valor x yo (\displaystyle x_(i)) en la muestra. Ya has encontrado las diferencias al cuadrado. (x yo (\displaystyle (x_(i))- X) 2 (\displaystyle ^(2)) para cada valor x yo (\displaystyle x_(i)) en la muestra; ahora solo suma estos cuadrados.
- En nuestro ejemplo: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
Divida el resultado por n - 1, donde n es el número de valores de la muestra. Hace algún tiempo, para calcular la varianza muestral, los estadísticos simplemente dividían el resultado entre n; en este caso obtendrás la media de la varianza al cuadrado, que es ideal para describir la varianza de una muestra determinada. Pero recuerde que cualquier muestra es sólo una pequeña parte de la población de valores. Si toma otra muestra y realiza los mismos cálculos, obtendrá un resultado diferente. Resulta que dividir por n - 1 (en lugar de solo n) da una estimación más precisa de la varianza de la población, que es lo que le interesa. La división por n – 1 se ha vuelto común, por lo que se incluye en la fórmula para calcular la varianza muestral.
- En nuestro ejemplo, la muestra incluye 6 valores, es decir, n = 6.
  Varianza muestral = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
La diferencia entre varianza y desviación estándar. Tenga en cuenta que la fórmula contiene un exponente, por lo que la dispersión se mide en unidades cuadradas del valor que se analiza. A veces es bastante difícil operar con tal magnitud; en tales casos, utilice la desviación estándar, que es igual a raíz cuadrada de la dispersión. Es por eso que la varianza muestral se denota como s 2 (\displaystyle s^(2)), y la desviación estándar de la muestra es como s (\displaystyle s).
- En nuestro ejemplo, la desviación estándar de la muestra es: s = √33,2 = 5,76.
Calcular la varianza de la población
1. Analizar algún conjunto de valores. El conjunto incluye todos los valores de la cantidad considerada. Por ejemplo, si estás estudiando la edad de los residentes Región de Leningrado, entonces la población incluye las edades de todos los residentes de esta área. Cuando se trabaja con una población, se recomienda crear una tabla e ingresar en ella los valores de la población. Considere el siguiente ejemplo:
  - En cierta habitación hay 6 acuarios. Cada acuario contiene la siguiente cantidad de peces:
    x 1 = 5 (\displaystyle x_(1)=5)
    x 2 = 5 (\displaystyle x_(2)=5)
    x 3 = 8 (\displaystyle x_(3)=8)
    x 4 = 12 (\displaystyle x_(4)=12)
    x 5 = 15 (\displaystyle x_(5)=15)
    x6 = 18 (\displaystyle x_(6)=18)
2. Escribe una fórmula para calcular la varianza poblacional. Dado que la totalidad incluye todos los valores de una determinada cantidad, la siguiente fórmula nos permite obtener valor exacto variaciones poblacionales. Para distinguir la varianza de la población de la varianza de la muestra (que es sólo una estimación), los estadísticos utilizan varias variables:
  - σ 2 (\displaystyle ^(2)) = (∑(x yo (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/norte
  - σ 2 (\displaystyle ^(2))– dispersión de la población (léase “sigma cuadrado”). La dispersión se mide en unidades cuadradas.
  - x yo (\displaystyle x_(i))– cada valor en total.
  - Σ – signo de suma. Es decir, de cada valor x yo (\displaystyle x_(i)) necesitas restar μ, elevarlo al cuadrado y luego sumar los resultados.
  - μ – media poblacional.
  - n – número de valores en la población.
3. Calcula la media poblacional. Cuando se trabaja con una población, su media se denota como μ (mu). La media poblacional se calcula como una media aritmética simple: suma todos los valores de la población y luego divide el resultado por el número de valores de la población.
  - Tenga en cuenta que los promedios no siempre se calculan como media aritmética.
  - En nuestro ejemplo, la media poblacional: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
4. Reste la media poblacional de cada valor de la población. Cuanto más cerca esté el valor de la diferencia de cero, más cerca estará el valor específico de la media poblacional. Encuentra la diferencia entre cada valor de la población y su media y tendrás una primera idea de la distribución de valores.
  - En nuestro ejemplo:
    x 1 (\displaystyle x_(1))- µ = 5 - 10,5 = -5,5
    x 2 (\displaystyle x_(2))- µ = 5 - 10,5 = -5,5
    x 3 (\displaystyle x_(3))- µ = 8 - 10,5 = -2,5
    x 4 (\displaystyle x_(4))- µ = 12 - 10,5 = 1,5
    x 5 (\displaystyle x_(5))- µ = 15 - 10,5 = 4,5
    x6 (\displaystyle x_(6))- µ = 18 - 10,5 = 7,5
5. Cuadra cada resultado obtenido. Los valores de diferencia serán tanto positivos como negativos; Si estos valores se trazan en una recta numérica, estarán a la derecha y a la izquierda de la media poblacional. Esto no es bueno para calcular la varianza porque los números positivos y negativos se cancelan entre sí. Así que eleva al cuadrado cada diferencia para obtener números exclusivamente positivos.
  - En nuestro ejemplo:
    (x yo (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) para cada valor de población (de i = 1 a i = 6):
    (-5,5)2 (\displaystyle ^(2)) = 30,25
    (-5,5)2 (\displaystyle ^(2)), Dónde x norte (\displaystyle x_(n))– el último valor de la población.
  - Para calcular el valor promedio de los resultados obtenidos, es necesario encontrar su suma y dividirla por n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x norte (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/norte
  - Ahora escribamos la explicación anterior usando variables: (∑( x yo (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n y obtenga una fórmula para calcular la varianza de la población.

Los principales indicadores generalizadores de variación en las estadísticas son las varianzas y los promedios. Desviación Estándar.

Dispersión esto significado aritmetico desviaciones al cuadrado de cada valor característico del promedio general. La varianza generalmente se denomina cuadrado medio de las desviaciones y se denota por  2. Dependiendo de los datos de origen, la varianza se puede calcular utilizando la media aritmética simple o ponderada:

 varianza no ponderada (simple);

 varianza ponderada.

Desviación Estándar esta es una característica generalizadora de los tamaños absolutos variaciones signos en conjunto. Se expresa en las mismas unidades de medida que el atributo (en metros, toneladas, porcentaje, hectáreas, etc.).

La desviación estándar es la raíz cuadrada de la varianza y se denota por :

 desviación estándar no ponderada;

 desviación estándar ponderada.

La desviación estándar es una medida de la confiabilidad de la media. Cuanto menor sea la desviación estándar, mejor refleja la media aritmética a toda la población representada.

El cálculo de la desviación estándar va precedido del cálculo de la varianza.

El procedimiento para calcular la varianza ponderada es el siguiente:

1) determinar la media aritmética ponderada:

2) calcular las desviaciones de las opciones del promedio:

3) eleva al cuadrado la desviación de cada opción del promedio:

4) multiplicar los cuadrados de las desviaciones por pesos (frecuencias):

5) resumir los productos resultantes:

6) la cantidad resultante se divide por la suma de los pesos:

Ejemplo 2.1

Calculemos la media aritmética ponderada:

Los valores de las desviaciones de la media y sus cuadrados se presentan en la tabla. Definamos la varianza:

La desviación estándar será igual a:

Si los datos de origen se presentan en forma de intervalo serie de distribución , primero debe determinar el valor discreto del atributo y luego aplicar el método descrito.

Ejemplo 2.2

Muestremos el cálculo de la varianza para una serie de intervalos utilizando datos sobre la distribución del área sembrada de una finca colectiva según el rendimiento del trigo.

La media aritmética es:

Calculemos la varianza:

6.3. Cálculo de la varianza mediante una fórmula basada en datos individuales.

Técnica de cálculo variaciones complicado, pero valores grandes Las opciones y frecuencias pueden ser abrumadoras. Los cálculos se pueden simplificar utilizando las propiedades de dispersión.

La dispersión tiene las siguientes propiedades.

1. Reducir o aumentar los pesos (frecuencias) de una característica variable un cierto número de veces no cambia la dispersión.

2. Disminuir o aumentar cada valor de una característica en la misma cantidad constante A no cambia la dispersión.

3. Disminuir o aumentar cada valor de una característica un cierto número de veces. k respectivamente reduce o aumenta la varianza en k 2 veces Desviación Estándar  en k una vez.

4. La dispersión de una característica con respecto a un valor arbitrario es siempre mayor que la dispersión con respecto a la media aritmética por cuadrado de la diferencia entre los valores promedio y arbitrarios:

Si A 0, entonces llegamos a la siguiente igualdad:

es decir, la varianza de la característica es igual a la diferencia entre el cuadrado medio de los valores característicos y el cuadrado de la media.

Cada propiedad se puede utilizar de forma independiente o en combinación con otras al calcular la varianza.

El procedimiento para calcular la varianza es simple:

1) determinar significado aritmetico :

2) eleva al cuadrado la media aritmética:

3) eleva al cuadrado la desviación de cada variante de la serie:

X i 2 .

4) encuentra la suma de cuadrados de las opciones:

5) dividir la suma de los cuadrados de las opciones por su número, es decir determinar el cuadrado promedio:

6) determinar la diferencia entre el cuadrado medio de la característica y el cuadrado de la media:

Ejemplo 3.1 Se dispone de los siguientes datos sobre la productividad de los trabajadores:

Hagamos los siguientes cálculos:

La dispersión en estadística se define como la desviación estándar de los valores individuales de una característica al cuadrado de la media aritmética. Un método común para calcular las desviaciones al cuadrado de las opciones del promedio y luego promediarlas.

En el análisis estadístico económico, se acostumbra evaluar la variación de una característica utilizando con mayor frecuencia la desviación estándar, es decir, la raíz cuadrada de la varianza;

(3)

Caracteriza la fluctuación absoluta de los valores de una característica variable y se expresa en las mismas unidades de medida que las opciones. En estadística, a menudo existe la necesidad de comparar la variación de diferentes características. Para tales comparaciones, se utiliza una medida relativa de variación, el coeficiente de variación.

Propiedades de dispersión:

1) si restas cualquier número de todas las opciones, la variación no cambiará;

2) si todos los valores de la opción se dividen por cualquier número b, entonces la varianza disminuirá b^2 veces, es decir

3) si calcula el cuadrado promedio de las desviaciones de cualquier número con una media aritmética desigual, entonces será mayor que la varianza. Al mismo tiempo, por un valor bien definido por cuadrado de la diferencia entre el valor medio c.

La dispersión se puede definir como la diferencia entre la media al cuadrado y la media al cuadrado.

17. Variaciones grupales e intergrupales. Regla de suma de varianza

Si una población estadística se divide en grupos o partes según la característica que se está estudiando, entonces se pueden calcular los siguientes tipos de dispersión para dicha población: grupo (privado), promedio grupal (privado) e intergrupal.

varianza total– refleja la variación de una característica debido a todas las condiciones y causas que operan en una población estadística determinada.

variación del grupo- igual al cuadrado medio de las desviaciones de los valores individuales de una característica dentro de un grupo de la media aritmética de este grupo, denominada media de grupo. Sin embargo, la media del grupo no coincide con la media general de toda la población.

La variación grupal refleja la variación de un rasgo sólo debido a condiciones y causas que operan dentro del grupo.

Promedio de variaciones del grupo- se define como la media aritmética ponderada de las varianzas del grupo, siendo los pesos los volúmenes del grupo.

Varianza intergrupal- igual al cuadrado medio de las desviaciones de los promedios grupales del promedio general.

La dispersión intergrupal caracteriza la variación de la característica resultante debido a la característica de agrupación.

Existe una cierta relación entre los tipos de dispersiones considerados: la dispersión total es igual a la suma de la dispersión promedio grupal e intergrupal.

Esta relación se llama regla de suma de varianzas.

18. Series dinámicas y sus componentes. Tipos de series temporales.

Fila en estadísticas- Se trata de datos digitales que muestran el cambio de un fenómeno en el tiempo o el espacio y permiten realizar una comparación estadística de los fenómenos tanto en el proceso de su desarrollo en el tiempo como en diversas formas y tipos de procesos. Gracias a esto, es posible detectar la dependencia mutua de los fenómenos.

En estadística, el proceso de desarrollo del movimiento de los fenómenos sociales a lo largo del tiempo se suele denominar dinámica. Para mostrar la dinámica se construyen series dinámicas (cronológicas, temporales), que son series de valores que varían en el tiempo de un indicador estadístico (por ejemplo, el número de condenados durante 10 años), ubicados en orden cronológico. Sus elementos constitutivos son los valores digitales de un indicador determinado y los períodos o momentos en el tiempo a los que se refieren.

La característica más importante de las series dinámicas.- su tamaño (volumen, magnitud) de un fenómeno particular logrado en un período determinado o en un momento determinado. En consecuencia, la magnitud de los términos de la serie dinámica es su nivel. Distinguir niveles inicial, medio y final de la serie dinámica. Primer nivel muestra el valor del primero, el final, el valor del último término de la serie. Nivel promedio representa el rango de variación cronológica promedio y se calcula dependiendo de si la serie dinámica es interválica o momentánea.

Otro característica importante series de tiempo- el tiempo transcurrido desde la observación inicial hasta la final, o el número de dichas observaciones.

Existen diferentes tipos de series temporales; se pueden clasificar según los siguientes criterios.

1) Dependiendo del método de expresión de los niveles, las series dinámicas se dividen en series de indicadores absolutos y derivados (valores relativos y medios).

2) Dependiendo de cómo los niveles de la serie expresen el estado del fenómeno en determinados momentos (al inicio de mes, trimestre, año, etc.) o su valor en determinados intervalos de tiempo (por ejemplo, por día, mes, año, etc.) etc.), distinguen entre series de dinámica de momento y de intervalo, respectivamente. Las series de momentos se utilizan relativamente raramente en el trabajo analítico de los organismos encargados de hacer cumplir la ley.

En teoría estadística, la dinámica se distingue según una serie de otros criterios de clasificación: según la distancia entre niveles, con niveles iguales y niveles desiguales en el tiempo; dependiendo de la presencia de la tendencia principal del proceso en estudio: estacionaria y no estacionaria. Al analizar series de tiempo, se parte de lo siguiente; los niveles de la serie se presentan en forma de componentes:

Y t = TP + E (t)

donde TP es un componente determinista que determina la tendencia general de cambio en el tiempo o tendencia.

E (t) es un componente aleatorio que provoca fluctuaciones en los niveles.

Para datos agrupados varianza residual - promedio de variaciones intragrupo:

Donde σ 2 j es la varianza intragrupo del jésimo grupo.

Para datos desagrupados varianza residual– medida de la precisión de la aproximación, es decir aproximación de la línea de regresión a los datos originales:
donde y(t) es el pronóstico utilizando la ecuación de tendencia; y t – serie dinámica inicial; n – número de puntos; p – número de coeficientes de la ecuación de regresión (número de variables explicativas).
En este ejemplo se llama estimador de varianza insesgado.

Ejemplo No. 1. La distribución de los trabajadores de tres empresas de una asociación según categorías arancelarias se caracteriza por los siguientes datos:

Categoría arancelaria obrero	Número de trabajadores en la empresa.
Categoría arancelaria obrero	empresa 1	empresa 2	empresa 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definir:
1. variación para cada empresa (variaciones intragrupo);
2. el promedio de las variaciones dentro del grupo;
3. dispersión intergrupal;
4. varianza total.

Solución.
Antes de empezar a solucionar el problema, es necesario averiguar qué característica es efectiva y cuál es factorial. En el ejemplo que nos ocupa, el atributo resultante es “Categoría arancelaria” y el atributo del factor es “Número (nombre) de la empresa”.
Luego tenemos tres grupos (empresas), para los cuales es necesario calcular el promedio del grupo y las variaciones intragrupo:

Compañía	promedio del grupo,	Variación dentro del grupo,
1	4	1,8

El promedio de las varianzas dentro del grupo ( varianza residual) se calculará mediante la fórmula:

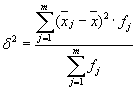
donde puedes calcular:

Entonces:
La varianza total será igual a: s 2 = 1,6 + 0 = 1,6.
La varianza total también se puede calcular utilizando una de las dos fórmulas siguientes:

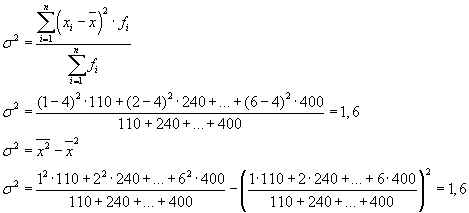
Al resolver problemas prácticos, a menudo uno tiene que lidiar con una característica que toma sólo dos valores alternativos. En este caso, no estamos hablando del peso de un valor particular de una característica, sino de su participación en la totalidad. Si la proporción de unidades de población que poseen la característica que se está estudiando se denota por " R", y los que no tienen - a través de " q", entonces la varianza se puede calcular usando la fórmula:
s2 = p×q

Ejemplo No. 2. Con base en los datos sobre la producción de seis equipos de trabajo, determine la varianza intergrupal y evalúe la influencia. turno de trabajo sobre su productividad laboral si la varianza total es 12,2.

Trabajador del equipo no.	Producción de trabajadores, uds.
Trabajador del equipo no.	en el primer turno	en el segundo turno
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Solución. Datos iniciales

X	f 1	f 2	f 3	f 4	f 5	f 6	Total
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Total	31	33	37	37	40	38

Luego tenemos 6 grupos para los cuales es necesario calcular la media grupal y las varianzas intragrupo.
1. Encuentra los valores promedio de cada grupo..

2. Encuentra el cuadrado medio de cada grupo..

Resumamos los resultados del cálculo en una tabla:

Número de grupo	Promedio del grupo	Variación dentro del grupo
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Variación dentro del grupo caracteriza el cambio (variación) de la característica estudiada (resultante) dentro de un grupo bajo la influencia de todos los factores sobre él, excepto el factor subyacente a la agrupación:
El promedio de las variaciones intragrupo se calculará mediante la fórmula:

4. Varianza intergrupal caracteriza el cambio (variación) de la característica estudiada (resultante) bajo la influencia de un factor (característica factorial) que forma la base del grupo.
Definimos la varianza intergrupal como:

Dónde

Entonces

varianza total caracteriza el cambio (variación) de la característica estudiada (resultante) bajo la influencia de todos los factores (características factoriales) sin excepción. Según las condiciones del problema, es igual a 12,2.
Relación de correlación empírica Mide qué parte de la variabilidad total de la característica resultante es causada por el factor que se está estudiando. Esta es la relación entre la varianza del factor y la varianza total:

Definimos la relación de correlación empírica:

Las conexiones entre características pueden ser débiles y fuertes (estrechas). Sus criterios se evalúan según la escala de Chaddock:
0,1 0,3 0,5 0,7 0,9 En nuestro ejemplo, la relación entre el rasgo Y y el factor X es débil
Coeficiente de determinación.

Determinemos el coeficiente de determinación:

Así, el 0,67% de la variación se debe a diferencias entre rasgos, y el 99,37% se debe a otros factores.
Conclusión: en este caso, la producción de los trabajadores no depende del trabajo en un turno específico, es decir la influencia del turno de trabajo en su productividad laboral no es significativa y se debe a otros factores.

Ejemplo No. 3. Basado en promedio salarios y al cuadrado de las desviaciones de su valor para dos grupos de trabajadores, encuentre la varianza total aplicando la regla de la suma de varianzas:

Solución:
Promedio de variaciones dentro del grupo

Definimos la varianza intergrupal como:

La varianza total será: 480 + 13824 = 14304