Un ejemplo de cálculo de expectativas matemáticas. Expectativa y varianza de una variable aleatoria.

Tarea 1. La probabilidad de germinación de las semillas de trigo es 0,9. ¿Cuál es la probabilidad de que de cuatro semillas sembradas broten al menos tres?

Solución. deja que el evento A– de 4 semillas brotarán al menos 3 semillas; evento EN– de 4 semillas brotarán 3 semillas; evento CON– de 4 semillas brotarán 4 semillas. Por el teorema de la suma de probabilidades.

Probabilidades
Y
determinado por la fórmula de Bernoulli utilizada en próximo caso. Que se lleve a cabo la serie. PAG pruebas independientes, durante cada una de las cuales la probabilidad de que ocurra el evento es constante e igual a R, y la probabilidad de que este evento no ocurra es igual a
. Entonces la probabilidad de que el evento A V PAG las pruebas aparecerán exactamente veces, calculado usando la fórmula de Bernoulli

,

Dónde
– número de combinaciones de PAG elementos por . Entonces

Probabilidad requerida

Tarea 2. La probabilidad de germinación de las semillas de trigo es 0,9. Calcula la probabilidad de que de 400 semillas sembradas, broten 350 semillas.

Solución. Calcular la probabilidad requerida
utilizar la fórmula de Bernoulli es difícil debido a lo engorroso de los cálculos. Por tanto, aplicamos una fórmula aproximada que expresa el teorema local de Laplace:

,

Dónde
Y
.

De las condiciones problemáticas. Entonces

.

De la tabla 1 de los apéndices encontramos. La probabilidad requerida es igual a

Tarea 3. Las semillas de trigo contienen un 0,02% de malas hierbas. ¿Cuál es la probabilidad de que si se seleccionan al azar 10 000 semillas se encuentren 6 semillas de malezas?

Solución. Aplicación del teorema local de Laplace debido a la baja probabilidad
conduce a una desviación significativa de la probabilidad de valor exacto
. Por lo tanto, a valores pequeños R calcular
aplicar la fórmula asintótica de Poisson

, Dónde .

Esta fórmula se utiliza cuando
, y cuanto menos R y más PAG, más preciso será el resultado.

Según las condiciones del problema.
;
. Entonces

Tarea 4. El porcentaje de germinación de las semillas de trigo es del 90%. Calcula la probabilidad de que de 500 semillas sembradas broten de 400 a 440 semillas.

Solución. Si la probabilidad de que ocurra un evento A en cada PAG las pruebas son constantes e iguales R, entonces la probabilidad
que el evento A en tales pruebas no habrá menos una vez y no más tiempos determinados por el teorema integral de Laplace mediante la siguiente fórmula:

, Dónde

,
.

Función
llamada función de Laplace. Los apéndices (Tabla 2) dan los valores de esta función para
. En
función
. Para valores negativos X debido a la rareza de la función de Laplace
. Usando la función de Laplace tenemos:

Según las condiciones de la tarea. Usando las fórmulas anteriores encontramos
Y :

Tarea 5. Se da la ley de distribución de una variable aleatoria discreta. X:

2. Encuentre: 1) expectativa matemática; 2) dispersión; 3) desviación estándar.

Solución. 1) Si la ley de distribución de discretos. variable aleatoria dado por tabla

2. Donde la primera línea contiene los valores de la variable aleatoria x y la segunda línea contiene las probabilidades de estos valores, entonces la expectativa matemática se calcula usando la fórmula

2) Variación
variable aleatoria discreta X se llama expectativa matemática de la desviación al cuadrado de una variable aleatoria de su expectativa matemática, es decir

Este valor caracteriza el valor promedio esperado de la desviación al cuadrado. X de
. De la última fórmula tenemos

Diferencia
se puede encontrar de otra manera, basándose en su siguiente propiedad: dispersión
igual a la diferencia entre la expectativa matemática del cuadrado de la variable aleatoria X y el cuadrado de su expectativa matemática
, eso es

Calcular
Dibujemos la siguiente ley de distribución de la cantidad.
:

3) Para caracterizar la dispersión de posibles valores de una variable aleatoria alrededor de su valor promedio, se introduce la desviación estándar
variable aleatoria X, igual raíz cuadrada de la variación
, eso es

.

De esta fórmula tenemos:

Tarea 6. Variable aleatoria continua X dada por la función de distribución acumulativa

Encuentre: 1) función de distribución diferencial
; 2) expectativa matemática
; 3) variación
.

Solución. 1) Función de distribución diferencial
variable aleatoria continua X se llama derivada de la función de distribución acumulativa
, eso es

.

La función diferencial buscada tiene la siguiente forma:

2) Si una variable aleatoria continua X dado por la función
, entonces su expectativa matemática está determinada por la fórmula

Desde la función
en
y en
es igual a cero, entonces de la última fórmula tenemos

.

3) Variación
lo determinaremos por la fórmula

Tarea 7. La longitud de la pieza es una variable aleatoria distribuida normalmente con una expectativa matemática de 40 mm y una desviación estándar de 3 mm. Encuentre: 1) la probabilidad de que la longitud de una pieza tomada arbitrariamente sea superior a 34 mm y inferior a 43 mm; 2) la probabilidad de que la longitud de la pieza se desvíe de su expectativa matemática en no más de 1,5 mm.

Solución. 1) dejar X– longitud de la pieza. Si la variable aleatoria X dado por una función diferencial
, entonces la probabilidad de que X tomará valores pertenecientes al segmento
, está determinado por la fórmula

.

Probabilidad de desigualdades estrictas
está determinada por la misma fórmula. Si la variable aleatoria X se distribuye según la ley normal, entonces

, (1)

Dónde
– función de Laplace,
.

En el problema. Entonces

2) Según las condiciones del problema, donde
. Sustituyendo en (1), tenemos

. (2)

De la fórmula (2) tenemos.

En el anterior presentamos una serie de fórmulas que nos permiten encontrar las características numéricas de funciones cuando se conocen las leyes de distribución de argumentos. Sin embargo, en muchos casos, para encontrar las características numéricas de funciones, no es necesario ni siquiera conocer las leyes de distribución de argumentos, sino que basta con conocer sólo algunas de sus características numéricas; al mismo tiempo, generalmente prescindimos de leyes de distribución. La determinación de las características numéricas de funciones a partir de determinadas características numéricas de los argumentos se utiliza ampliamente en la teoría de la probabilidad y puede simplificar significativamente la solución de una serie de problemas. La mayoría de estos métodos simplificados se relacionan con funciones lineales; sin embargo, algunas funciones no lineales elementales también permiten un enfoque similar.

En el presente presentaremos una serie de teoremas sobre las características numéricas de funciones, que en conjunto representan un aparato muy simple para calcular estas características, aplicable en una amplia gama de condiciones.

1. Valor esperado valor no aleatorio

La propiedad formulada es bastante obvia; se puede probar considerando una variable no aleatoria como un tipo especial de aleatoria, con un valor posible con probabilidad uno; luego según la fórmula general de la expectativa matemática:

.

2. Dispersión de una variable no aleatoria

Si es un valor no aleatorio, entonces

3. Sustituir el signo de expectativa matemática por un valor no aleatorio

, (10.2.1)

es decir, se puede tomar un valor no aleatorio como signo de la expectativa matemática.

Prueba.

a) Para cantidades discontinuas

b) Para cantidades continuas

.

4. Sustituir el signo de dispersión y la desviación estándar por un valor no aleatorio

Si es una cantidad no aleatoria y es aleatoria, entonces

, (10.2.2)

es decir, se puede sacar un valor no aleatorio del signo de la dispersión elevándolo al cuadrado.

Prueba. Por definición de varianza

Consecuencia

,

es decir, un valor no aleatorio se puede sacar del signo de la desviación estándar por su valor absoluto. La demostración la obtenemos sacando la raíz cuadrada de la fórmula (10.2.2) y teniendo en cuenta que el r.s.o. - un valor significativamente positivo.

5. Expectativa matemática de la suma de variables aleatorias.

Demostremos que para dos variables aleatorias cualesquiera y

es decir, la expectativa matemática de la suma de dos variables aleatorias es igual a la suma de sus expectativas matemáticas.

Esta propiedad se conoce como teorema de la suma de expectativas matemáticas.

Prueba.

a) Sea un sistema de variables aleatorias discontinuas. Apliquemos la fórmula general (10.1.6) a la suma de variables aleatorias para la expectativa matemática de una función de dos argumentos:

.

Ho representa nada más que la probabilidad total de que la cantidad tome el valor:

;

por eso,

.

De manera similar demostraremos que

,

y el teorema está demostrado.

b) Sea un sistema de variables aleatorias continuas. Según la fórmula (10.1.7)

. (10.2.4)

Transformemos la primera de las integrales (10.2.4):

;

similarmente

,

y el teorema está demostrado.

Cabe señalar especialmente que el teorema para sumar expectativas matemáticas es válido para cualquier variable aleatoria, tanto dependiente como independiente.

El teorema para sumar expectativas matemáticas se generaliza a un número arbitrario de términos:

, (10.2.5)

es decir, la expectativa matemática de la suma de varias variables aleatorias es igual a la suma de sus expectativas matemáticas.

Para comprobarlo basta utilizar el método de inducción completa.

6. Expectativa matemática función lineal

Considere una función lineal de varios argumentos aleatorios:

donde están los coeficientes no aleatorios. Probemos que

, (10.2.6)

es decir, la expectativa matemática de una función lineal es igual a la misma función lineal de las expectativas matemáticas de los argumentos.

Prueba. Usando el teorema de la suma de m.o. y la regla de colocar una cantidad no aleatoria fuera del signo del m.o., obtenemos:

.

7. Dispensarepisodioesta suma de variables aleatorias

La varianza de la suma de dos variables aleatorias es igual a la suma de sus varianzas más el doble del momento de correlación:

Prueba. denotemos

Según el teorema de la suma de expectativas matemáticas.

Pasemos de las variables aleatorias a las correspondientes variables centradas. Restando la igualdad (10.2.9) término por término de la igualdad (10.2.8), tenemos:

Por definición de varianza

Q.E.D.

La fórmula (10.2.7) para la varianza de la suma se puede generalizar a cualquier número de términos:

, (10.2.10)

donde es el momento de correlación de las cantidades, el signo debajo de la suma significa que la suma se extiende a todas las posibles combinaciones por pares de variables aleatorias .

La prueba es similar a la anterior y se desprende de la fórmula del cuadrado de un polinomio.

La fórmula (10.2.10) se puede escribir de otra forma:

, (10.2.11)

donde la doble suma se extiende a todos los elementos de la matriz de correlación del sistema de cantidades , que contiene momentos de correlación y varianzas.

Si todas las variables aleatorias , incluidos en el sistema, no están correlacionados (es decir, cuando ), la fórmula (10.2.10) toma la forma:

, (10.2.12)

es decir, la varianza de la suma de variables aleatorias no correlacionadas es igual a la suma de las varianzas de los términos.

Esta posición se conoce como teorema de la suma de varianzas.

8. Varianza de una función lineal

Consideremos una función lineal de varias variables aleatorias.

donde están las cantidades no aleatorias.

Demostremos que la dispersión de esta función lineal se expresa mediante la fórmula

, (10.2.13)

donde es el momento de correlación de las cantidades , .

Prueba. Introduzcamos la notación:

. (10.2.14)

Aplicando la fórmula (10.2.10) para la dispersión de la suma al lado derecho de la expresión (10.2.14) y teniendo en cuenta que , obtenemos:

¿Dónde está el momento de correlación de las cantidades?

.

Calculemos este momento. Tenemos:

;

similarmente

Sustituyendo esta expresión en (10.2.15), llegamos a la fórmula (10.2.13).

En el caso especial cuando todas las cantidades no están correlacionados, la fórmula (10.2.13) toma la forma:

, (10.2.16)

es decir, la varianza de una función lineal de variables aleatorias no correlacionadas es igual a la suma de los productos de los cuadrados de los coeficientes y las varianzas de los argumentos correspondientes.

9. Expectativa matemática de un producto de variables aleatorias.

La expectativa matemática del producto de dos variables aleatorias es igual al producto de sus expectativas matemáticas más el momento de correlación:

Prueba. Partiremos de la definición del momento de correlación:

Transformemos esta expresión usando las propiedades de la expectativa matemática:

que obviamente es equivalente a la fórmula (10.2.17).

Si las variables aleatorias no están correlacionadas, entonces la fórmula (10.2.17) toma la forma:

es decir, la expectativa matemática del producto de dos variables aleatorias no correlacionadas es igual al producto de sus expectativas matemáticas.

Esta posición se conoce como teorema de la multiplicación de expectativas matemáticas.

La fórmula (10.2.17) no es más que una expresión del segundo momento central mixto del sistema a través del segundo momento inicial mixto y expectativas matemáticas:

. (10.2.19)

Esta expresión se utiliza a menudo en la práctica al calcular el momento de correlación de la misma manera que para una variable aleatoria la varianza a menudo se calcula a través del segundo momento inicial y la expectativa matemática.

El teorema de la multiplicación de expectativas matemáticas se generaliza a un número arbitrario de factores, solo que en este caso, para su aplicación, no basta con que las cantidades no estén correlacionadas, sino que se requiere que algunos momentos mixtos superiores, cuyo número depende en el número de términos en el producto, desaparecen. Estas condiciones ciertamente se cumplen si las variables aleatorias incluidas en el producto son independientes. En este caso

, (10.2.20)

es decir, la expectativa matemática del producto de variables aleatorias independientes es igual al producto de sus expectativas matemáticas.

Esta proposición puede demostrarse fácilmente mediante inducción completa.

10. Varianza del producto de variables aleatorias independientes

Demostremos que para cantidades independientes

Prueba. Denotemos. Por definición de varianza

Como las cantidades son independientes y

Cuando son independientes, las cantidades también lo son; por eso,

,

Pero no existe más que el segundo momento inicial de la magnitud, y, por tanto, se expresa a través de la dispersión:

;

similarmente

.

Sustituyendo estas expresiones en la fórmula (10.2.22) y reuniendo términos similares, llegamos a la fórmula (10.2.21).

En el caso de multiplicar variables aleatorias centradas (variables con expectativas matemáticas iguales a cero), la fórmula (10.2.21) toma la forma:

, (10.2.23)

es decir, la varianza del producto de variables aleatorias centradas independientes es igual al producto de sus varianzas.

11. Momentos superiores de la suma de variables aleatorias.

En algunos casos es necesario calcular los momentos más altos de la suma de variables aleatorias independientes. Probemos algunas relaciones relacionadas aquí.

1) Si las cantidades son independientes, entonces

Prueba.

de donde, según el teorema de la multiplicación de expectativas matemáticas

Pero el primer momento central de cualquier cantidad es cero; los dos términos intermedios desaparecen y se demuestra la fórmula (10.2.24).

La relación (10.2.24) se generaliza fácilmente por inducción a un número arbitrario de términos independientes:

. (10.2.25)

2) El cuarto momento central de la suma de dos variables aleatorias independientes se expresa mediante la fórmula

donde están las variaciones de las cantidades y .

La prueba es completamente similar a la anterior.

Utilizando el método de inducción completa, es fácil demostrar la generalización de la fórmula (10.2.26) a un número arbitrario de términos independientes.

La expectativa matemática de una variable aleatoria discreta es la suma de los productos de todos sus valores posibles y sus probabilidades.

Supongamos que una variable aleatoria toma solo valores de probabilidad que sean respectivamente iguales. Entonces la expectativa matemática de una variable aleatoria está determinada por la igualdad.

Si una variable aleatoria discreta toma un conjunto contable de valores posibles, entonces

Además, la expectativa matemática existe si la serie del lado derecho de la igualdad converge absolutamente.

Comentario. De la definición se deduce que la expectativa matemática de una variable aleatoria discreta es una cantidad no aleatoria (constante).

Definición de expectativa matemática en el caso general.

Determinemos la expectativa matemática de una variable aleatoria cuya distribución no es necesariamente discreta. Empecemos con el caso de las variables aleatorias no negativas. La idea será aproximar dichas variables aleatorias utilizando variables discretas para las cuales ya se ha determinado la expectativa matemática, y establecer la expectativa matemática igual al límite de las expectativas matemáticas de las variables aleatorias discretas que la aproximan. Por cierto, esta es una idea general muy útil, que es que alguna característica se determina primero para objetos simples y luego, para objetos más complejos, se determina acercándolos a otros más simples.

Lema 1. Sea una variable aleatoria arbitraria no negativa. Entonces existe una secuencia de variables aleatorias discretas tal que

Prueba. Dividamos el semieje en segmentos de igual longitud y determinemos

Entonces las propiedades 1 y 2 se derivan fácilmente de la definición de una variable aleatoria, y

Lema 2. Sea una variable aleatoria no negativa y dos secuencias de variables aleatorias discretas que poseen las propiedades 1-3 del Lema 1. Entonces

Prueba. Tenga en cuenta que para variables aleatorias no negativas permitimos

En virtud de la Propiedad 3, es fácil ver que existe una secuencia de números positivos tal que

Resulta que

Usando las propiedades de las expectativas matemáticas para variables aleatorias discretas, obtenemos

Pasando al límite en obtenemos el enunciado del Lema 2.

Definición 1. Sea una variable aleatoria no negativa, una secuencia de variables aleatorias discretas que tienen las propiedades 1-3 del Lema 1. La expectativa matemática de una variable aleatoria es el número

El lema 2 garantiza que no depende de la elección de la secuencia aproximada.

Sea ahora una variable aleatoria arbitraria. definamos

De la definición se deduce fácilmente que

Definición 2. La expectativa matemática de una variable aleatoria arbitraria es el número

Si al menos uno de los números del lado derecho de esta igualdad es finito.

Propiedades de la expectativa matemática

Propiedad 1. La expectativa matemática de un valor constante es igual a la constante misma:

Prueba. Consideraremos una constante como una variable aleatoria discreta que tiene un valor posible y lo toma con probabilidad, por lo tanto,

Observación 1. Definamos el producto de una variable constante por una variable aleatoria discreta como un aleatorio discreto cuyos valores posibles son iguales a los productos de la constante por los valores posibles; las probabilidades de los valores posibles son iguales a las probabilidades de los valores posibles correspondientes. Por ejemplo, si la probabilidad de un valor posible es igual entonces la probabilidad de que el valor tome el valor también es igual.

Propiedad 2. El factor constante se puede sacar del signo de la expectativa matemática:

Prueba. Sea la variable aleatoria dada por la ley de distribución de probabilidad:

Teniendo en cuenta la observación 1, escribimos la ley de distribución de la variable aleatoria.

Observación 2. Antes de pasar a la siguiente propiedad, señalamos que dos variables aleatorias se llaman independientes si la ley de distribución de una de ellas no depende de los posibles valores que tomó la otra variable. De lo contrario, las variables aleatorias son dependientes. Varias variables aleatorias se denominan mutuamente independientes si las leyes de distribución de cualquier número de ellas no dependen de los posibles valores que tomaron las variables restantes.

Observación 3. Definamos el producto de variables aleatorias independientes y como variable aleatoria cuyos valores posibles son iguales a los productos de cada valor posible por cada valor posible, las probabilidades de los valores posibles del producto son iguales a los productos de las probabilidades de los valores posibles de los factores. Por ejemplo, si la probabilidad de un valor posible es, la probabilidad de un valor posible es entonces la probabilidad de un valor posible es

Propiedad 3. La expectativa matemática del producto de dos variables aleatorias independientes es igual al producto de sus expectativas matemáticas:

Prueba. Dejemos que las variables aleatorias independientes se especifiquen mediante sus propias leyes de distribución de probabilidad:

Recopilemos todos los valores que puede tomar una variable aleatoria. Para ello multipliquemos todos los valores posibles por cada valor posible; Como resultado, obtenemos y, teniendo en cuenta la Observación 3, escribimos la ley de distribución, asumiendo por simplicidad que todos los valores posibles del producto son diferentes (si este no es el caso, entonces la prueba se realiza en un manera similar):

La expectativa matemática es igual a la suma de los productos de todos los valores posibles y sus probabilidades:

Consecuencia. La expectativa matemática del producto de varias variables aleatorias mutuamente independientes es igual al producto de sus expectativas matemáticas.

Propiedad 4. La expectativa matemática de la suma de dos variables aleatorias es igual a la suma de las expectativas matemáticas de los términos:

Prueba. Dejemos que se den las variables aleatorias. las siguientes leyes distribuciones:

Recopilemos todos los valores posibles de una cantidad. Para ello, sumamos cada valor posible a cada valor posible; obtenemos, por simplicidad, supongamos que estos valores posibles son diferentes (si este no es el caso, entonces la prueba se realiza de manera similar), y denotamos sus probabilidades, respectivamente, por y.

La esperanza matemática de un valor es igual a la suma de los productos de valores posibles y sus probabilidades:

Demostremos que un evento que tomará el valor (la probabilidad de este evento es igual) implica un evento que tomará el valor o (la probabilidad de este evento según el teorema de la suma es igual), y viceversa. De ahí se sigue que las igualdades se prueban de manera similar.

Sustituyendo los lados derechos de estas igualdades en la relación (*), obtenemos

o finalmente

Varianza y desviación estándar

En la práctica, a menudo es necesario estimar la dispersión de posibles valores de una variable aleatoria alrededor de su valor medio. Por ejemplo, en artillería es importante saber qué tan cerca caerán los proyectiles del objetivo que se va a alcanzar.

A primera vista, puede parecer que la forma más sencilla de estimar la dispersión es calcular todas las desviaciones posibles de una variable aleatoria y luego encontrar su valor promedio. Sin embargo, este camino no dará nada, ya que el valor medio de la desviación, es decir, para cualquier variable aleatoria es igual a cero. Esta propiedad se explica por el hecho de que algunas posibles desviaciones son positivas, mientras que otras son negativas; como resultado de su cancelación mutua, el valor de desviación promedio es cero. Estas consideraciones indican la conveniencia de sustituir las posibles desviaciones por sus valores absolutos o sus cuadrados. Esto es lo que hacen en la práctica. Es cierto que en el caso de que las posibles desviaciones se reemplacen por valores absolutos, hay que operar con valores absolutos, lo que a veces conduce a graves dificultades. Por lo tanto, la mayoría de las veces toman un camino diferente, es decir, Calcule el valor promedio de la desviación al cuadrado, que se llama dispersión.

2. Conceptos básicos de la teoría de la probabilidad.

Valor esperado

Considere una variable aleatoria con valores numéricos. A menudo resulta útil asociar un número con esta función: su "valor medio" o, como dicen, " valor promedio", "índice de tendencia central". Por diversas razones, algunas de las cuales quedarán claras más adelante, la expectativa matemática suele utilizarse como “valor promedio”.

Definición 3. Expectativa matemática de una variable aleatoria. X número llamado

aquellos. la expectativa matemática de una variable aleatoria es una suma ponderada de los valores de una variable aleatoria con pesos iguales a las probabilidades de los eventos elementales correspondientes.

Ejemplo 6. Calculemos la expectativa matemática del número que aparece en la cara superior del dado. Se deduce directamente de la Definición 3 que

Declaración 2. Deja que la variable aleatoria X toma valores x 1, x 2,…, xmetro. Entonces la igualdad es verdadera.

(5)

aquellos. La expectativa matemática de una variable aleatoria es una suma ponderada de los valores de la variable aleatoria con pesos iguales a las probabilidades de que la variable aleatoria tome ciertos valores.

A diferencia de (4), donde la suma se realiza directamente sobre eventos elementales, un evento aleatorio puede constar de varios eventos elementales.

A veces se toma la relación (5) como definición de expectativa matemática. Sin embargo, utilizando la Definición 3, como se muestra a continuación, es más fácil establecer las propiedades de la expectativa matemática necesaria para construir modelos probabilísticos de fenómenos reales que utilizando la relación (5).

Para probar la relación (5), agrupamos en (4) términos con valores idénticos de la variable aleatoria:

Dado que el factor constante se puede quitar del signo de la suma, entonces

Determinando la probabilidad de un evento.

Usando las dos últimas relaciones obtenemos lo requerido:

El concepto de expectativa matemática en la teoría estadística-probabilística corresponde al concepto de centro de gravedad en mecánica. Pongámoslo en puntos. x 1, x 2,…, xmetro en el eje del número de masa PAG(X= X 1 ), PAG(X= X 2 ),…, PAG(X= x m) respectivamente. Entonces la igualdad (5) muestra que el centro de gravedad de este sistema de puntos materiales coincide con la expectativa matemática, lo que muestra la naturalidad de la Definición 3.

Declaración 3. Dejar X- valor aleatorio, M(X)– su expectativa matemática, A– un cierto número. Entonces

1) M(a)=a; 2) M(X-M(X))=0; 3M[(X- a) 2 ]= METRO[(X- METRO(X)) 2 ]+(a- METRO(X)) 2 .

Para probar esto, consideremos primero una variable aleatoria que es constante, es decir la función mapea el espacio de eventos elementales a un solo punto A. Dado que el multiplicador constante se puede llevar más allá del signo de la suma, entonces

Si cada miembro de una suma se divide en dos términos, entonces la suma total se divide en dos sumas, de las cuales la primera está formada por los primeros términos y la segunda por el segundo. Por lo tanto, la expectativa matemática de la suma de dos variables aleatorias X+Y, definido en el mismo espacio de eventos elementales, es igual a la suma de expectativas matemáticas M(X) Y METRO(U) estas variables aleatorias:

M(X+Y) = M(X) + M(Y).

Y por lo tanto M(X-M(X)) = M(X) - M(M(X)). Como se muestra arriba, M(M(X)) = M(X). Por eso, M(X-M(X)) = M(X) - M(X) = 0.

Porque el (X - a) 2 = ((X – METRO(X)) + (METRO(X) - a)} 2 = (X - METRO(X)) 2 + 2(X - METRO(X))(METRO(X) - a) + (METRO(X) – a) 2 , Eso METRO[(X - a) 2 ] =METRO(X - METRO(X)) 2 + METRO{2(X - METRO(X))(METRO(X) - a)} + METRO[(METRO(X) – a) 2 ]. Simplifiquemos la última igualdad. Como se muestra al comienzo de la prueba del enunciado 3, la expectativa matemática de una constante es la constante misma y, por lo tanto, METRO[(METRO(X) – a) 2 ] = (METRO(X) – a) 2 . Dado que el factor constante se puede eliminar más allá del signo de la suma, entonces METRO{2(X - METRO(X))(METRO(X) - a)} = 2(METRO(X) - a)METRO(X - METRO(X)). El lado derecho de la última igualdad es 0 porque, como se muestra arriba, M(X-M(X))=0. Por eso, METRO[(X- a) 2 ]= METRO[(X- METRO(X)) 2 ]+(a- METRO(X)) 2 , que era lo que había que demostrar.

De lo anterior se deduce que METRO[(X- a) 2 ] alcanza un mínimo A, igual METRO[(X- METRO(X)) 2 ], en a = M(X), ya que el segundo término en la igualdad 3) siempre es no negativo y es igual a 0 solo para el valor especificado A.

Declaración 4. Deja que la variable aleatoria X toma valores x 1, x 2,…, xmetro, y f es alguna función del argumento numérico. Entonces

Para demostrar esto, agrupemos en el lado derecho de la igualdad (4), que define la expectativa matemática, términos con los mismos valores:

Utilizando el hecho de que el factor constante se puede sacar del signo de la suma y la definición de la probabilidad de un evento aleatorio (2), obtenemos

Q.E.D.

Declaración 5. Dejar X Y Ud.– variables aleatorias definidas en el mismo espacio de eventos elementales, A Y b- algunos números. Entonces METRO(hacha+ por)= soy(X)+ bm(Y).

Usando la definición de la expectativa matemática y las propiedades del símbolo de suma, obtenemos una cadena de igualdades:

Se ha demostrado lo requerido.

Lo anterior muestra cómo la expectativa matemática depende de la transición a otro punto de referencia y a otra unidad de medida (transición Y=hacha+b), así como a funciones de variables aleatorias. Los resultados obtenidos se utilizan constantemente en análisis técnicos y económicos, en la evaluación de las actividades económicas y financieras de una empresa, durante la transición de una moneda a otra en cálculos económicos extranjeros, en documentación reglamentaria y técnica, etc. Los resultados considerados permiten uso de las mismas fórmulas de cálculo para varios parámetros de escala y desplazamiento.

Anterior

La expectativa y la varianza son las características numéricas más utilizadas de una variable aleatoria. Caracterizan las características más importantes de la distribución: su posición y grado de dispersión. En muchos problemas prácticos, una característica completa y exhaustiva de una variable aleatoria (la ley de distribución) no se puede obtener en absoluto o no es necesaria en absoluto. En estos casos, uno se limita a una descripción aproximada de una variable aleatoria utilizando características numéricas.

El valor esperado a menudo se denomina simplemente valor promedio de una variable aleatoria. La dispersión de una variable aleatoria es una característica de la dispersión, la dispersión de una variable aleatoria alrededor de su expectativa matemática.

Expectativa de una variable aleatoria discreta

Acerquémonos al concepto de expectativa matemática, basándonos primero en la interpretación mecánica de la distribución de una variable aleatoria discreta. Sea la unidad de masa distribuida entre los puntos del eje x. X1 , X 2 , ..., X norte, y cada punto material tiene una masa correspondiente de pag1 , pag 2 , ..., pag norte. Es necesario seleccionar un punto en el eje de abscisas, caracterizando la posición de todo el sistema de puntos materiales, teniendo en cuenta sus masas. Es natural tomar como tal punto el centro de masa del sistema de puntos materiales. Este es el promedio ponderado de la variable aleatoria. X, a la que la abscisa de cada punto Xi entra con un “peso” igual a la probabilidad correspondiente. El valor medio de la variable aleatoria obtenido de esta forma. X se llama expectativa matemática.

La expectativa matemática de una variable aleatoria discreta es la suma de los productos de todos sus valores posibles y las probabilidades de estos valores:

Ejemplo 1. Se ha organizado una lotería en la que todos ganan. Hay 1000 ganancias, de las cuales 400 son 10 rublos. 300 - 20 rublos cada uno. 200 - 100 rublos cada uno. y 100 - 200 rublos cada uno. ¿Cuál es la ganancia promedio de alguien que compra un boleto?

Solución. Encontraremos las ganancias promedio si dividimos la cantidad total de ganancias, que es 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rublos, por 1000 (cantidad total de ganancias). Entonces obtenemos 50000/1000 = 50 rublos. Pero la expresión para calcular las ganancias promedio se puede presentar de la siguiente forma:

Por otro lado, en estas condiciones, la cantidad ganadora es una variable aleatoria, que puede tomar valores de 10, 20, 100 y 200 rublos. con probabilidades iguales a 0,4, respectivamente; 0,3; 0,2; 0.1. Por lo tanto, el pago promedio esperado igual a la suma productos del tamaño de las ganancias y la probabilidad de recibirlas.

Ejemplo 2. El editor decidió publicar. Nuevo libro. Planea vender el libro por 280 rublos, de los cuales él mismo recibirá 200, 50 - la librería y 30 - el autor. La tabla proporciona información sobre los costos de publicar un libro y la probabilidad de vender una cierta cantidad de copias del libro.

Encuentre la ganancia esperada del editor.

Solución. La variable aleatoria “beneficio” es igual a la diferencia entre los ingresos por ventas y el costo de los costos. Por ejemplo, si se venden 500 copias de un libro, los ingresos por la venta son 200 * 500 = 100 000 y el costo de publicación es 225 000 rublos. Por tanto, el editor se enfrenta a una pérdida de 125.000 rublos. La siguiente tabla resume los valores esperados de la variable aleatoria - beneficio:

Número	Ganancia Xi	Probabilidad pagi	Xi pag i
500	-125000	0,20	-25000
1000	-50000	0,40	-20000
2000	100000	0,25	25000
3000	250000	0,10	25000
4000	400000	0,05	20000
Total:		1,00	25000

Así, obtenemos la expectativa matemática del beneficio del editor:

.

Ejemplo 3. Probabilidad de acertar de un solo tiro. pag= 0,2. Determinar el consumo de proyectiles que proporcionen una expectativa matemática del número de impactos igual a 5.

Solución. A partir de la misma fórmula matemática de expectativa que hemos usado hasta ahora, expresamos X- consumo de cáscara:

.

Ejemplo 4. Determinar la expectativa matemática de una variable aleatoria. X número de aciertos con tres disparos, si la probabilidad de acierto con cada disparo pag = 0,4 .

Sugerencia: encuentre la probabilidad de valores de variables aleatorias por La fórmula de Bernoulli. .

Propiedades de la expectativa matemática

Consideremos las propiedades de la expectativa matemática.

Propiedad 1. La expectativa matemática de un valor constante es igual a esta constante:

Propiedad 2. El factor constante se puede sacar del signo de expectativa matemática:

Propiedad 3. La expectativa matemática de la suma (diferencia) de variables aleatorias es igual a la suma (diferencia) de sus expectativas matemáticas:

Propiedad 4. La expectativa matemática de un producto de variables aleatorias es igual al producto de sus expectativas matemáticas:

Propiedad 5. Si todos los valores de una variable aleatoria X disminuir (aumentar) en el mismo número CON, entonces su expectativa matemática disminuirá (aumentará) en el mismo número:

Cuando no puedes limitarte solo a las expectativas matemáticas

En la mayoría de los casos, sólo la expectativa matemática no puede caracterizar suficientemente una variable aleatoria.

Deja que las variables aleatorias X Y Y están dadas por las siguientes leyes de distribución:

Significado X	Probabilidad
-0,1	0,1
-0,01	0,2
0	0,4
0,01	0,2
0,1	0,1

Significado Y	Probabilidad
-20	0,3
-10	0,1
0	0,2
10	0,1
20	0,3

Las expectativas matemáticas de estas cantidades son las mismas: iguales a cero:

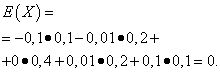
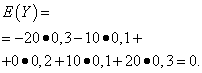
Sin embargo, sus patrones de distribución son diferentes. Valor aleatorio X sólo puede tomar valores que difieren poco de la expectativa matemática, y la variable aleatoria Y Puede tomar valores que se desvíen significativamente de la expectativa matemática. Un ejemplo similar: el salario medio no permite juzgar Gravedad específica trabajadores con salarios altos y bajos. En otras palabras, a partir de la expectativa matemática no se puede juzgar qué desviaciones de ella, al menos en promedio, son posibles. Para hacer esto, necesitas encontrar la varianza de la variable aleatoria.

Varianza de una variable aleatoria discreta

Diferencia variable aleatoria discreta X se llama expectativa matemática del cuadrado de su desviación de la expectativa matemática:

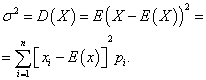
La desviación estándar de una variable aleatoria. X el valor aritmético de la raíz cuadrada de su varianza se llama:

.

Ejemplo 5. Calcular varianzas y medias. desviaciones estandar variables aleatorias X Y Y, cuyas leyes de distribución se dan en las tablas anteriores.

Solución. Expectativas matemáticas de variables aleatorias. X Y Y, como se encontró arriba, son iguales a cero. Según la fórmula de dispersión en mi(X)=mi(y)=0 obtenemos:

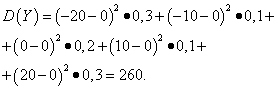
Entonces las desviaciones estándar de variables aleatorias. X Y Y constituir

.

Así, con las mismas expectativas matemáticas, la varianza de la variable aleatoria X muy pequeña, pero una variable aleatoria Y- significativo. Esto es consecuencia de diferencias en su distribución.

Ejemplo 6. El inversor tiene 4 proyectos de inversión alternativos. La tabla resume el beneficio esperado en estos proyectos con la probabilidad correspondiente.

Proyecto 1	Proyecto 2	Proyecto 3	Proyecto 4
500, PAG=1	1000, PAG=0,5	500, PAG=0,5	500, PAG=0,5
	0, PAG=0,5	1000, PAG=0,25	10500, PAG=0,25
		0, PAG=0,25	9500, PAG=0,25

Encuentre la expectativa matemática, la varianza y la desviación estándar para cada alternativa.

Solución. Muestremos cómo se calculan estos valores para la tercera alternativa:

La tabla resume los valores encontrados para todas las alternativas.

Todas las alternativas tienen las mismas expectativas matemáticas. Esto significa que a la larga todos tienen los mismos ingresos. La desviación estándar se puede interpretar como una medida del riesgo: cuanto mayor sea, mayor será el riesgo de la inversión. Un inversor que no quiera correr mucho riesgo elegirá el proyecto 1 ya que tiene la desviación estándar más pequeña (0). Si el inversor prefiere el riesgo y una alta rentabilidad en un período corto, elegirá el proyecto con la mayor desviación estándar: el proyecto 4.

Propiedades de dispersión

Presentemos las propiedades de la dispersión.

Propiedad 1. La varianza de un valor constante es cero:

Propiedad 2. El factor constante se puede sacar del signo de dispersión elevándolo al cuadrado:

.

Propiedad 3. La varianza de una variable aleatoria es igual a la expectativa matemática del cuadrado de este valor, del cual se resta el cuadrado de la expectativa matemática del valor mismo:

,

Dónde .

Propiedad 4. La varianza de la suma (diferencia) de variables aleatorias es igual a la suma (diferencia) de sus varianzas:

Ejemplo 7. Se sabe que una variable aleatoria discreta X toma sólo dos valores: −3 y 7. Además, se conoce la expectativa matemática: mi(X) = 4 . Encuentra la varianza de una variable aleatoria discreta.

Solución. Denotemos por pag la probabilidad con la que una variable aleatoria toma un valor X1 = −3 . Entonces la probabilidad del valor X2 = 7 será 1 - pag. Derivemos la ecuación para la expectativa matemática:

mi(X) = X 1 pag + X 2 (1 − pag) = −3pag + 7(1 − pag) = 4 ,

donde obtenemos las probabilidades: pag= 0,3 y 1 − pag = 0,7 .

Ley de distribución de una variable aleatoria:

X	−3	7
pag	0,3	0,7

Calculamos la varianza de esta variable aleatoria usando la fórmula de la propiedad 3 de dispersión:

D(X) = 2,7 + 34,3 − 16 = 21 .

Encuentre usted mismo la expectativa matemática de una variable aleatoria y luego observe la solución

Ejemplo 8. Variable aleatoria discreta X toma sólo dos valores. Acepta el mayor de los valores 3 con probabilidad 0,4. Además, se conoce la varianza de la variable aleatoria. D(X) = 6 . Encuentre la expectativa matemática de una variable aleatoria.

Ejemplo 9. En la urna hay 6 bolas blancas y 4 negras. De la urna se extraen 3 bolas. El número de bolas blancas entre las bolas extraídas es una variable aleatoria discreta. X. Encuentre la expectativa matemática y la varianza de esta variable aleatoria.

Solución. Valor aleatorio X puede tomar valores 0, 1, 2, 3. Las probabilidades correspondientes se pueden calcular a partir de regla de multiplicación de probabilidad. Ley de distribución de una variable aleatoria:

X	0	1	2	3
pag	1/30	3/10	1/2	1/6

De ahí la expectativa matemática de esta variable aleatoria:

METRO(X) = 3/10 + 1 + 1/2 = 1,8 .

La varianza de una variable aleatoria dada es:

D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .

Expectativa y varianza de una variable aleatoria continua.

Para una variable aleatoria continua, la interpretación mecánica de la expectativa matemática conservará el mismo significado: el centro de masa de una unidad de masa distribuida continuamente en el eje x con densidad F(X). A diferencia de una variable aleatoria discreta, cuyo argumento de función Xi cambia abruptamente; para una variable aleatoria continua, el argumento cambia continuamente. Pero la expectativa matemática de una variable aleatoria continua también está relacionada con su valor promedio.

Para encontrar la expectativa matemática y la varianza de una variable aleatoria continua, necesitas encontrar integrales definidas . Si se da la función de densidad de una variable aleatoria continua, entonces entra directamente en el integrando. Si se da una función de distribución de probabilidad, al diferenciarla, es necesario encontrar la función de densidad.

La media aritmética de todos los valores posibles de una variable aleatoria continua se llama expectativa matemática, denotado por o .